3. Leviathan Hangi Problemi Çözer?
Bir önceki yazıda Hobbes’un Leviathan fikrini ve ona getirilen eleştirileri ele almış, iktisatçı jargonuyla özgürlüğü, barışın temini için devlete ödenen risk primi olarak değerlendirmiştik. Şimdiye kadar devlete dair tartışmamızı bireylerin kendi başlarına ve diğerlerinin kararını önemsemeksizin karar aldığını varsayarak yürütmüştük. Kişilerin başkalarının kararından bağımsız, riskten kaçınmaya yatkın olduğunu ve ve gelecekteki olası riskleri azaltmak adına özgürlüklerinden vazgeçerek Leviathan’ı oluşturduklarını ifade etmiştik.
Buradan sonraki kısımda isimde kişilerin birbirleriyle stratejik etkileşim içerisinde olduğu durumda, başka bir deyişle kişilerin kararlarının diğerlerinin kararına bağlı olarak belirlendiği bir ortamda oyun teorisinin bize öğrettiği temel enstrümanları ve analiz tekniklerini kullanarak devlet meselesini ele almaya çalışacağım.
Oyun teorisi, basitçe ajan diye tabir edilen karar vericilerin diğer ajanların kararlarını dikkate alarak karar verdikleri durumları inceler. Stratejik ilişki derken bu tip durumları ifade ediyoruz.
Yazılar arasında kopukluğa sebebiyet vermemek adına tekrara düşmeyi göze alarak önceki yazıda bahsi geçen Hobbes’a ait fikirleri iktisatçı jargonuyla ele almak istiyorum. Demiştik ki, Hobbes’un doğa durumundan eşitlik ve özgürlük ilkeleri vasıtasıyla meydana gelen yıkıcı savaş ortamından kaçınmak için bireyler otoriteye ihtiyaç duyar ve devlet, bu kanal üzerinden meşruiyetini elde eder. Otoriteye ihtiyaç vardır çünkü Hobbes’a göre kişinin sözüne güvenilmez. İnsanlar, birbirlerine verdikleri sözleri tutmazlar, bu sebeple de kendi aralarında sürdürülebilir bir anlaşmayı tesis edemezler ve anlaşmanın devamlılığı için bir otoriteye ihtiyaç duyarlar. Aslında Hobbes’un bu bakışını oyun kuramcıları o çok meşhur Mahkum İkilemi oyunu ile ifade ederler. Ben bu oyunu “Mutabakat Oyunu” olarak isimlendiriyorum.
Bir oyunu analiz edebilmemiz için dört temel bilgiye ihtiyaç duyarız: Oyuncuların kim oldukları, hangi seçeneklerinin olduğu, sonuçlardan ne kadar fayda elde edecekleri ve oyuncuların sahip olduğu bilgidir. Bu oyunu, Hobbes’un doğa durumuna dair betimlemesine uygun olarak modifiye edip sunacağım.
Varsayalım ki toplumda iki karar alıcı kişi (Vatandaş A ve Vatandaş B) ve her birinin iki seçeneği (Barış ve Saldırı) olsun. Olası durumlardan elde edecekleri faydalar da kutuların içindeki rakamlar ile ifade edilsin. Oyun eşzamanlı bir biçimde oynanıyor olsun ve her iki oyuncu da olası sonuçların her iki tarafa da ne getireceğini biliyor olsun. Oyun basitçe şu şekilde oluşacaktır:
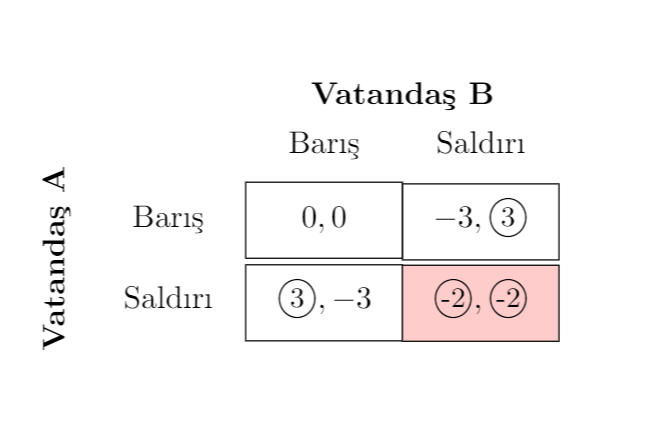
Şimdi A oyuncusunun, B oyuncusunun olası hamlelerine karşı en iyi tepkilerine bakalım. Yuvarlak içine aldıklarım, bu en iyi tepkileri göstermektedir. En iyi tepki derken şunu kastetmekteyim: Eğer B oyuncusu Barış’ı seçerse, A oyuncusu Barış’ı seçtiği takdirde 0 fayda elde edecekken, Saldırı’yı seçtiği takdirde 3 fayda elde edecekti. Demek ki, B oyuncusunun Barış tercihine karşı A oyuncusunun en iyi tepkisi, Saldırı olmaktadır. Eğer B oyuncusu Saldırı’yı seçmiş olsa idi, A oyuncusu Barış’ı seçtiği takdirde -3 fayda alacakken, Saldırı’yı seçtiği takdirde -2 fayda alacaktır. Sonuç olarak, B oyuncusu neyi seçerse seçsin, A oyuncusunun en iyi tepkisi Saldırı’dır ve biz buna dominant strateji adını veriyoruz. Oyun simetrik olduğu için, B oyuncusu için de dominant strateji Saldırı’dır.
Bu aşamada Nash Dengesini tanımlamaya hazırız. Çok basitçe, Nash Dengesi, en iyi tepkilerin kesiştiği noktadır. Daha formal bir tanımla, hiçbir oyuncu için, diğer oyuncuların tercihlerini sabitlediğimizde daha karlı bir tercih bulamıyorsak Nash Dengesi’ndeyiz demektir.
Yukarıdaki oyun formunda, en iyi tepkilerin kesiştiği yer, (Saldırı, Saldırı) durumudur ve mutabakat oyunundaki tek Nash dengesi burasıdır. Formal tanım üzerinden düşünecek olursak, karşı tarafın saldırısına dair en iyi tepkim saldırıdır, bu karşı taraf için de böyledir ve (Saldırı, Saldırı) hali Nash Dengesi’dir. (Saldırı, Saldırı) halini Hobbes’un doğa durumu diye tabir ettiği savaş hali olarak düşündüğümüzü hatırlatmak isterim. Daha açık bir şekilde ifade edersek, Hobbes’un doğa durumu diye tabir ettiği, bizim (Saldırı, Saldırı) diye tabir ettiğimiz savaş hali, bireyleri özgür ve kendi halinde bıraktığımızda gerçekleşecek olan durumdur. Yani, insanlar rasyonel biçimde kendi çıkarlarını düşündüklerinde, savaş durumu kaçınılmazdır ve her iki taraf da bundan zarar görür.
Şimdi, şunu sormaya başlıyoruz. Eğer barış hali (Barış , Barış) seçilseydi? Kolaylıkla görebiliriz ki bu durum, savaş haline göre her iki oyuncu için de daha iyi bir netice üretecekti. Biz iktisatçılar, bu durumu Pareto dominasyon olarak isimlendiriyoruz. Eğer kimseyi kötü yapmadan en az bir kişiyi daha iyi bir sonuca ulaştırabiliyorsam, orada Pareto dominasyon var demektir. Savaş hali her iki oyuncuya da barış haline nazaran daha fazla fayda getirmektedir demek ki barış hali, savaş halini Pareto-domine etmektedir. Pareto-domine edilemeyen dağılımları da Pareto Etkin olarak tabir ediyoruz. Detayları kaybetmek pahasına bunu Toplumsal En İyi sonuç olarak da ele alabiliriz. Sonuçta, savaş hali, barış hali tarafından Pareto domine edildiği için, savaş hali Pareto etkin değildir. Mahkum İkileminin, bizim isimlendirmemizde Mutabakat Oyununun, temel sonucuna yeni ulaşabildik. Nash Dengesi, bu oyunda Pareto etkin değildir.
Barış hali, her iki kişi için de savaş haline göre daha iyidir dedik. Peki neden insanlar saldırıyı seçerler ve savaş hali Nash Dengesi olur? Daha isabetli sorarsak, neden Pareto etkin olan barış hali Nash Dengesi değildir? Cevabımız çok basit. Korku. Siz, barışı seçseniz dahi, karşı tarafın size saldıracak olacak olması, sizi saldırmayı tercih etmeye zorlar ve her iki oyuncu da bu şekilde düşündüğü için savaş hali ortaya çıkar. İnsan, enayi durumuna düşmekten korkar da diyebiliriz.
Bu oyun neden çok kuvvetlidir? Adam Smith der ki, herkes kendi çıkarının peşinde koşarsa, toplum için en iyi sonuç elde edilir. Bu oyun ise bize söyler ki, herkesin kendi çıkarının peşinde koştuğu durumda, toplum için en iyi sonuç elde edilmez. Kişilerin birbirine karşı güvensizliği onları herkes için daha kötü bir sonuca götürür.
Yukarıda Mutabakat Oyunu diye adlandırdığımız Mahkum İkilemi olarak bilinen oyunu, iki kişi yerine N kişinin oynadığını düşünelim. Toplumu oluşturan fertlerin büyük sayıda olduğu düşünüldüğünde, oyunu bu şekilde düşünmek gerekir. Fark edeceğiniz üzere, böyle bir oyunu bir matris şeklinde ifade etmemiz mümkün değil. Daha anlaşılır kılmak için, N-kişili statik bir Mahkum İkilemi oyunu ile eşdeğer olan, Tragedy of Commonsolarak bilinen, Ortak Malların Trajedisi olarak çevirebileceğimiz, oyunu sunmak istiyorum.
Buradaki ortak malı, Toroslardaki bir köyün hayvan yetiştiricilerinin kullandığı ortak mera olarak düşünelim. Hayvan sayısı ne kadar artarsa, meranın kapasitesi o kadar düşecektir. Kendinizi hayvancılık yapan bir köylü olarak hayal edin. Diğer herkesin hayvan sayısı tercihini sabit kabul ettiğinizde, sizin bir tane daha hayvanı meraya sokmanız, meranın verimini neredeyse düşürmeyecektir. Yani sizin en iyi tepkiniz, diğerleri ne kadar hayvan seçerse seçsin, her zaman daha fazla hayvanı meraya sokmak olacaktır. Problem şu ki, sizin yaptığınız ve düşündüğünüz şeyi herkes yaparsa, mera yok olacaktır. Yani ortak kullanılan bir malın, bireysel çıkar uğruna hoyratça kullanılması ve bunu herkesin yapıyor olması, ortak malı yok edecektir. Aynı örneği çevre kirliliği bağlamında da düşünebiliriz.

Aslında bu N kişi, kendi arasında kooperasyon kurabilseydi, merayı usulünce kullanacak ve herkes daha iyi bir sonuç elde edecekti. Sonuç itibariyle, yine Nash Dengesinin Pareto etkin olmadığını görüyoruz. Kişilerin bu davranışını iktisatçılar free-rider problem (bedavacılık problemi) olarak adlandırıyorlar. Özetle, siz birilerinin ortak alanı kötüye kullanarak fayda sağlayacağını düşünerek, siz de kötüye kullanırsınız ve ve ortak malın akıbeti trajediyle sonuçlanır.
Bir başka örnek olarak, bir fabrikada çalışan işçilerin çalışma şartlarını iyileştirmek için greve gitme durumunu ele alalım. Greve ne kadar çok işçi katılırsa, grevin başarılı olma ihtimali artacaktır. Ancak grev başarısız olursa, işçi işten atılacaktır. Herkesin aynı anda karar verdiğini düşünürsek, diğerleri ne yaparsa yapsın, buradaki dominant strateji, greve katılmamaktır. Herkes greve katılmış olsa dahi, grevin başarılı olduğu durumdaki iyileşmeden herkes faydalanacağı için, diğerlerinin katılmadığı başarısız bir grev girişiminin sonunda işten atılma riskini göz önüne alarak greve katılmamak dominant stratejidir. Böylece hiç kimse greve katılmaz. Yine görüyoruz ki, Nash Dengesi Pareto Etkin değildir. Herkes greve katılsaydı, herkesin durumu iyileşecekti. Bedavacılık problemiyle çok benzer bir biçimde bu problemi de collective action problem (kolektif hareket problemi) olarak adlandırıyoruz. Detayına girmemekle beraber, son günlerde yaşanan Reddit’te örgütlenerek finansal piyasaları alt üst eden hareketi de kolektif hareket problemi bağlamında ele alabiliriz ki o kitlenin bu problemi nasıl çözdüğü benim için hala açık bir soru.
Bütün bu örneklerle beraber, görüyoruz ki, kişilerin kendi çıkarının peşinde koşması, Adam Smith’in dediğinin aksine toplumsal en iyi sonucu üretemiyor. Demek ki toplumun kooperasyonu tesis edebilmesi için başka türlü mekanizmalar geliştirmesi gerekiyor. Bu meseleyi ileride daha derinleştireceğiz.
Sonuç itibariyle en baştaki tartışmamıza dönecek olursak, Nash Dengesi, yahut olacak olan, yahut bireylerin kendi çıkarını gözeterek yaptığı tercihler, Pareto etkin sonucu üretemiyor. Herkesi daha iyiye ulaştıracak kooperasyonu, içimizdeki bedavacılar yüzünden kuramayız. Öyleyse, içimizdeki bedavacıları cezalandırmamız gerekir ki bu sebeple Leviathan’ı yaratırız. Biz, toplum olarak, kendi aramızda kooperasyonu sağlayamadığımız için üçüncü parti ceza uygulayıcısı olarak devlete ihtiyaç duyarız. Bu bahsi, şu şekilde sonlandırabiriz: Hobbes için devlet, bireyleri Nash Dengesinden (savaş durumundan) Pareto etkin olana (barış durumuna) taşıyan mekanizmanın adıdır.
Bu yazıyla beraber, Leviathan’ın hangi problemi çözerek meşruiyet kazandığını görmüş olduk diye düşünüyorum. Bir sonraki yazıda, Leviathan’ın bu problemi nasıl çözdüğünü ufak modifikasyonlarla göstermeyi ve ardından bu çözümün beraberinde getirdiği maliyetitartışmayı istiyorum.
Bir sonraki yazıda görüşmek dileğiyle…
